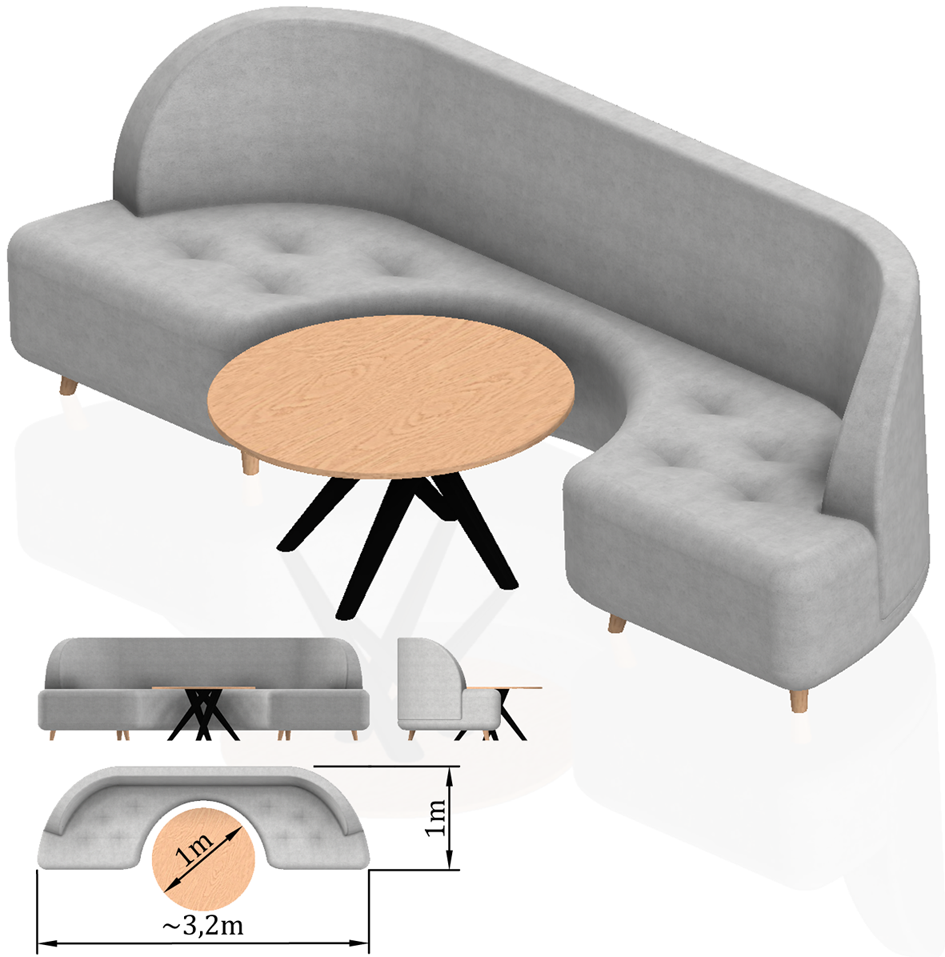
What is the optimal shape of sofa?

Used tools and packages

Matlab Differential geometry Optimization Toolbox

Introduction

This project results from my interest in math. What is the largest area of region that can be moved through a ninety-degree corner in a hallway of unit width? - this problem called "the moving sofa problem" was formulated for the first time by Moser and till now has not been solved fully. The essence is to find such a shape of the maximum area that can be moved around a ninety-degree corner while a planar case is under consideration. The simplicity of the formulation of the problem, which allows anyone to understand it, and advanced calculation techniques used for analyses have retained the scientific interest of researchers until today. One of the first proposed solutions was a sofa built from circular arcs and straight lines, the area of which was A_H=π/2+2/π=2.2074... . However, this solution was not optimal, as proved by Gerver, who proposed a sofa with the area A_G=2.2195316688... constructed from 18 analytically defined curves. This solution was probably the optimum one, though it has not yet been proven globally. Here I give the method that may be used to analyze this problem and to construct proof that indeed Gerver sofa is the optimum one.

Sofa generation

Fixed coordinate system h was established, in which the region of hallway $H = {(x_{h}, y_{h}) \in R^{2} : y_{h} \leq | x_{h} | + \sqrt{2} \land y_{h} \geq | x_{h} |}$ is bounded by two curves parametrised as ${\bar{r}}_{u}^{(h)} = {[x_{u}^{(h)} (t_{u}), y_{u}^{(h)} (t_{u})]}^{T}$ and ${\bar{r}}_{l}^{(h)} = {[x_{l}^{(h)} (t_{l}), y_{l}^{(h)} (t_{l})]}^{T}$ (Fig. below)

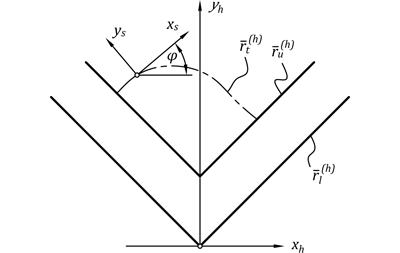
Position vectors of the upper and lower boundaries of the hallway are expressed by:

{\bar{r}}_{u}^{(h)} (t_{u}) = [\begin{array}{cc} x_{u}^{(h)} \\ y_{u}^{(h)} \end{array}] = [\begin{array}{cc} t_{u} \\ | t_{u} | + \sqrt{2} \end{array}]

{\bar{r}}_{l}^{(h)} (t_{l}) = [\begin{array}{cc} x_{l}^{(h)} \\ y_{l}^{(h)} \end{array}] = [\begin{array}{cc} t_{l} \\ | t_{l} | \end{array}]

where t_u i t_l are the hallway's parameters. Moreover, coordinate system s connected with the sofa moves along the trajectory defined by a parametric curve in the form of ${\bar{r}}_{t}^{(h)} = {[x_{t}^{(h)} (t_{t}) y_{t}^{(h)} (t_{t})]}^{T}$ and rotates by $φ (t_{t})$ , where t_t is the parameter of the path of movement. In order to express the hallway's boundaries in the coordinate system connected with the sofa, we may use:

{\bar{r}}_{u, l}^{(s)} = [\begin{matrix} \cos φ & \sin φ \\ - \sin φ & \cos φ \end{matrix}] \cdot ([\begin{matrix} x_{u, l}^{(h)} \\ y_{u, l}^{(h)} \end{matrix}] + [\begin{matrix} x_{t}^{(h)} \\ - y_{t}^{(h)} \end{matrix}])

where indexes u and l refer to the upper and lower boundaries of the hallway, respectively. This equation describes one parameter family of curves with parameter t_t. After transformation, we obtain:

{\bar{r}}_{u}^{(s)} = [\begin{matrix} x_{u}^{(s)} \\ y_{u}^{(s)} \end{matrix}] = [\begin{matrix} \cos φ (x_{t}^{(h)} + x_{u}^{(h)}) + \sin φ (y_{t}^{(h)} - y_{u}^{(h)}) \\ \sin φ (x_{t}^{(h)} + x_{u}^{(h)}) - \cos φ (y_{t}^{(h)} - y_{u}^{(h)}) \end{matrix}]

{\bar{r}}_{l}^{(s)} = [\begin{matrix} x_{l}^{(s)} \\ y_{l}^{(s)} \end{matrix}] = [\begin{matrix} \cos φ (x_{t}^{(h)} + x_{l}^{(h)}) + \sin φ (y_{t}^{(h)} - y_{l}^{(h)}) \\ \sin φ (x_{t}^{(h)} + x_{l}^{(h)}) - \cos φ (y_{t}^{(h)} - y_{l}^{(h)}) \end{matrix}]

The necessary condition for the existence of envelopes expressed as the perpendicularity of the vector normal and a derivative of the vector of a family of curves with respect to its parameter takes the form of:

f_{u} (t_{u}, t_{t}) = \frac{\partial x_{u}^{(s)}}{\partial t_{t}} \cdot \frac{\partial y_{u}^{(s)}}{\partial t_{u}} - \frac{\partial x_{u}^{(s)}}{\partial t_{u}} \cdot \frac{\partial y_{u}^{(s)}}{\partial t_{t}} = 0

f_{l} (t_{l}, t_{t}) = \frac{\partial x_{l}^{(s)}}{\partial t_{t}} \cdot \frac{\partial y_{l}^{(s)}}{\partial t_{l}} - \frac{\partial x_{l}^{(s)}}{\partial t_{l}} \cdot \frac{\partial y_{l}^{(s)}}{\partial t_{t}} = 0

calculating the partial derivatives and putting them into above equations, we arrive at the envelopes:

f_{u} (t_{u}, t_{t}) = \frac{\partial x_{t}^{(h)}}{\partial t_{t}} \pm \frac{\partial y_{t}^{(h)}}{\partial t_{t}} \mp \sqrt{2} \frac{\partial φ}{\partial t_{t}} - 2 \frac{\partial φ}{\partial t_{t}} t_{u} - \frac{\partial φ}{\partial t_{t}} x_{t}^{(h)} \pm \frac{\partial φ}{\partial t_{t}} y_{t}^{(h)} = 0

f_{l} (t_{l}, t_{t}) = \frac{\partial x_{t}^{(h)}}{\partial t_{t}} \pm \frac{\partial y_{t}^{(h)}}{\partial t_{t}} - 2 \frac{\partial φ}{\partial t_{t}} t_{l} - \frac{\partial φ}{\partial t_{t}} x_{t}^{(h)} \pm \frac{\partial φ}{\partial t_{t}} y_{t}^{(h)} = 0

wherein the upper sign stands for the right-hand side and the lower sign stands for the left-hand side. The solutions to above equations, with the assumption that $\partial φ / \partial t_{t} \neq 0$ , are:

t_{u} = \pm \frac{1}{2 \frac{\partial φ}{\partial t_{t}}} (\frac{\partial x_{t}^{(h)}}{\partial t_{t}} \pm \frac{\partial y_{t}^{(h)}}{\partial t_{t}} - \sqrt{2} \frac{\partial φ}{\partial t_{t}} \mp \frac{\partial φ}{\partial t_{t}} x_{t}^{(h)} + \frac{\partial φ}{\partial t_{t}} y_{t}^{(h)})

t_{l} = \pm \frac{1}{2 \frac{\partial φ}{\partial t_{t}}} (\frac{\partial x_{t}^{(h)}}{\partial t_{t}} \pm \frac{\partial y_{t}^{(h)}}{\partial t_{t}} \mp \frac{\partial φ}{\partial t_{t}} x_{t}^{(h)} + \frac{\partial φ}{\partial t_{t}} y_{t}^{(h)})

Taking into account the above results in family of curves, we obtain the envelopes of the consecutive positions of the hallway boundaries in the sofa's coordinate system:

{\bar{r}}_{s u}^{(s)} (t_{t}) = {\bar{r}}_{u}^{(s)} (t_{u} (t_{t}), t_{t})

{\bar{r}}_{s l}^{(s)} (t_{t}) = {\bar{r}}_{l}^{(s)} (t_{l} (t_{t}), t_{t})

The above equations stand while the derivatives $\partial {\bar{r}}_{u}^{(h)} / \partial t_{u}$ and $\partial {\bar{r}}_{l}^{(h)} / \partial t_{l}$ exist. Otherwise, as for point t_u=0, the envelope can be represented by the curve defined as:

{\bar{r}}_{s c u}^{(s)} (t_{t}) = {\bar{r}}_{u}^{(s)} (t_{u} = 0, t_{t})

Assuming that the sofa's path of movement and angle of rotation are given in a discrete way as a set of points $x_{t_{i}}^{(h)}$ , $y_{t_{i}}^{(h)}$ and $φ_{i}$ , where i=1,2,...,n, and taking finite differences quotients instead of derivatives, solutions to envelope equations can be expressed as:

t_{u_{i}} = \pm \frac{1}{2 Δ φ_{i}} (Δ x_{t_{i}}^{(h)} \pm Δ y_{t_{i}}^{(h)} - \sqrt{2} Δ φ_{i} \mp Δ φ_{i} x_{t_{i}}^{(h)} + Δ φ_{i} y_{t_{i}}^{(h)})

t_{l_{i}} = \pm \frac{1}{2 Δ φ_{i}} (Δ x_{t_{i}}^{(h)} \pm Δ y_{t_{i}}^{(h)} \mp Δ φ_{i} x_{t_{i}}^{(h)} + Δ φ_{i} y_{t_{i}}^{(h)})

The discrete representation of curves which bound the region of sofa are therefore established as:

{\bar{r}}_{s u_{i}}^{(s)} = [\begin{matrix} x_{s u_{i}}^{(s)} \\ y_{s u_{i}}^{(s)} \end{matrix}] = [\begin{matrix} \cos φ_{i} (x_{t_{i}}^{(h)} + t_{u_{i}}) + \sin φ_{i} (y_{t_{i}}^{(h)} - (\pm t_{u_{i}} + \sqrt{2})) \\ \sin φ_{i} (x_{t_{i}}^{(h)} + t_{u_{i}}) - \cos φ_{i} (y_{t_{i}}^{(h)} - (\pm t_{u_{i}} + \sqrt{2})) \end{matrix}]

{\bar{r}}_{s l_{i}}^{(s)} = [\begin{matrix} x_{s l_{i}}^{(s)} \\ y_{s l_{i}}^{(s)} \end{matrix}] = [\begin{matrix} \cos φ_{i} (x_{t_{i}}^{(h)} + t_{l_{i}}) + \sin φ (y_{t_{i}}^{(h)} \mp t_{l_{i}}) \\ \sin φ_{i} (x_{t_{i}}^{(h)} + t_{l_{i}}) - \cos φ (y_{t_{i}}^{(h)} \mp t_{l_{i}}) \end{matrix}]

{\bar{r}}_{s c u_{i}}^{(s)} = [\begin{matrix} x_{s c u_{i}}^{(s)} \\ y_{s c u_{i}}^{(s)} \end{matrix}] = [\begin{matrix} x_{t_{i}}^{(h)} \cos φ_{i} + \sin φ_{i} (y_{t_{i}}^{(h)} - \sqrt{2}) \\ x_{t_{i}}^{(h)} \sin φ_{i} - \cos φ_{i} (y_{t_{i}}^{(h)} - \sqrt{2}) \end{matrix}]

Finally, it can be said that the region of sofa is $S = {(x_{s}, y_{s}) \in R^{2} : y_{s} \leq y_{s u_{i}}^{(s)} \land y_{s} \geq y_{s l_{i}}^{(s)} \land y_{s} \leq y_{s c u_{i}}^{(s)}}$ , where it should be within the region limited by the initial and the final position of the hallway $S \subseteq B = {(x_{s}, y_{s}) \in R^{2} : y_{s} \leq y_{u_{1}}^{(s)} \land y_{s} \leq y_{u_{n}}^{(s)} \land y_{s} \geq y_{l_{1}}^{(s)} \land y_{s} \geq y_{l_{n}}^{(s)} \land x_{s} \geq x_{l_{1}}^{(s)} \land x_{s} \leq x_{l_{n}}^{(s)}}$ , where:

\begin{matrix} y_{u_{1}}^{(s)} = \sin φ_{1} (x_{t_{1}}^{(h)} + t_{u}) - \cos φ_{1} (y_{t_{1}}^{(h)} - (| t_{u} | + \sqrt{2})), \\ y_{u_{n}}^{(s)} = \sin φ_{n} (x_{t_{n}}^{(h)} + t_{u}) - \cos φ_{n} (y_{t_{n}}^{(h)} - (| t_{u} | + \sqrt{2})), \\ x_{l_{1}}^{(s)} = \cos φ_{1} (x_{t_{1}}^{(h)} + t_{l}) + \sin φ_{1} (y_{t_{1}}^{(h)} - | t_{l} |), \\ y_{l_{1}}^{(s)} = \sin φ_{1} (x_{t_{1}}^{(h)} + t_{l}) - \cos φ_{1} (y_{t_{1}}^{(h)} - | t_{l} |), \\ x_{l_{n}}^{(s)} = \cos φ_{n} (x_{t_{n}}^{(h)} + t_{l}) + \sin φ_{n} (y_{t_{n}}^{(h)} - | t_{l} |), \\ y_{l_{n}}^{(s)} = \sin φ_{n} (x_{t_{n}}^{(h)} + t_{l}) - \cos φ_{n} (y_{t_{n}}^{(h)} - | t_{l} |) . \end{matrix}

The shape of the sofa is obtained based on discrete curves bounding its region by means of standard curve intersection detection algorithms. The area of the sofa can be calculated as the area of a polygon with multiple numbers of sides; if the symmetrical case is considered in order to accelerate the calculations, they can be run for half of the sofa only.

Results

Gerver's sofa:

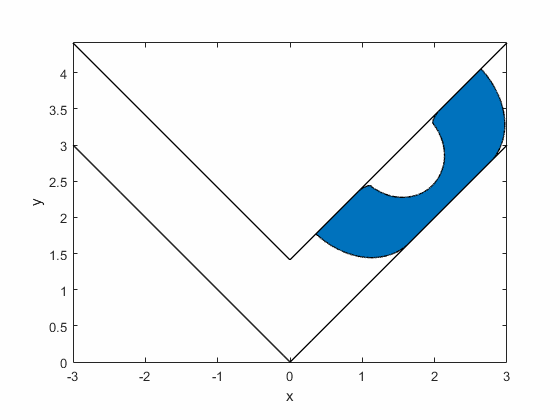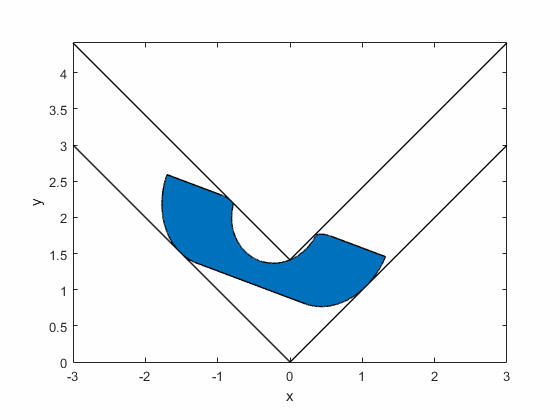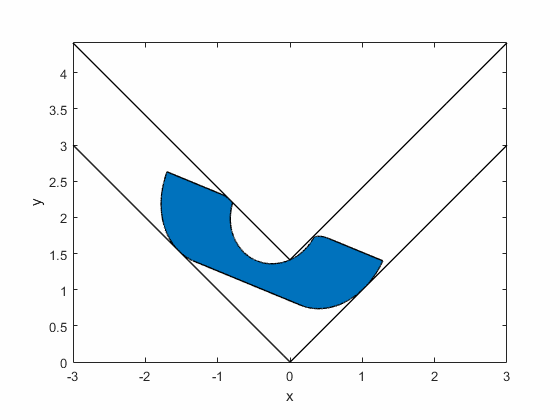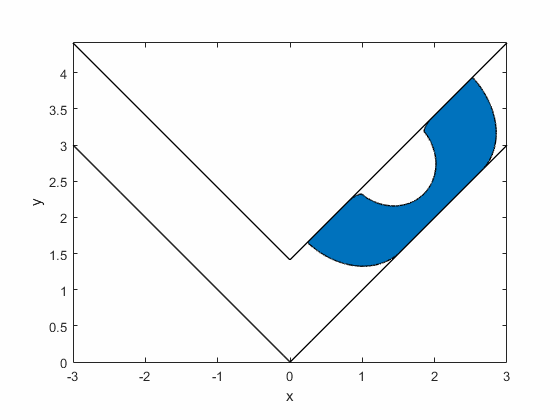
Romik's ambidextrous sofa:

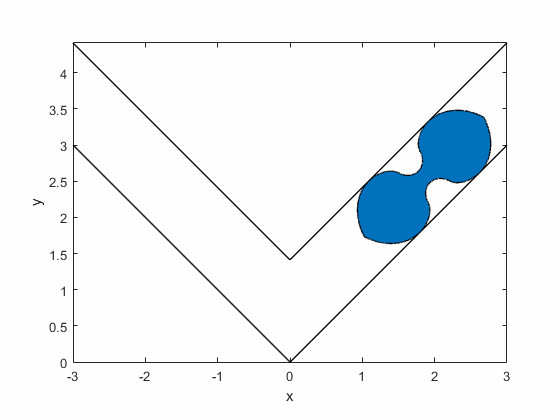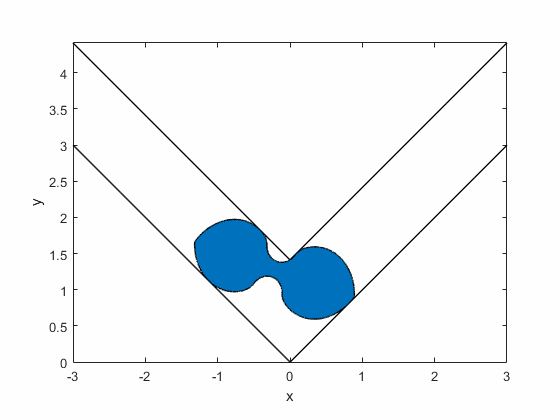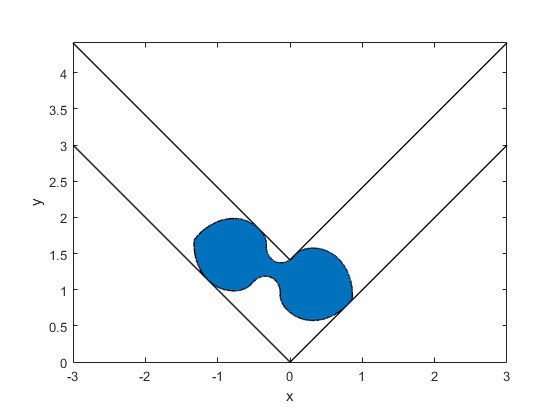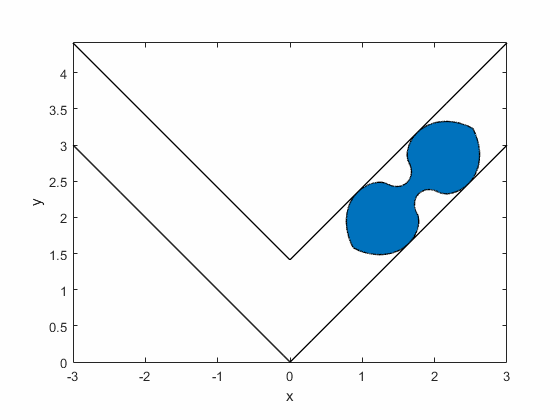
Summary

Proposed method may be successfully used for generating sofas. Moreover, the method could be used for designing a mathematical model in which functions of the path of movement and the angle of rotation are obtained in order to maximise the sofa's area. Another potential application of the designed method is to prove that a truly optimal solution must be symmetrical. For that purpose, one can formulate a functional describing the area of the sofa and construct a proof that the extremum is only reached when the path of movement is symmetric and there is an odd parity of the angle of rotation (in other words, the sofa is symmetric). One can try to achieve this by undermining, on the basis of the above assumptions, the system of Euler equations, which is a necessary condition for the existence of an extremum. Nevertheless, the sofa with the maximum area is that proposed by Gerver; not only is it highly likely to be the optimal solution to the posed problem, but it is also possible to design a neat piece of furniture offering space for rather a large coffee table:

← Back to projects ↑ Back on top